Pressure

Given that the expansion of air inside the bottle is adiabatic and there is a rapid expansion of the air inside the bottle, we can also use the following equation to calculate the pressure exerted by the air inside the bottle. We are assuming the nozzle has a diameter of 22 mm.

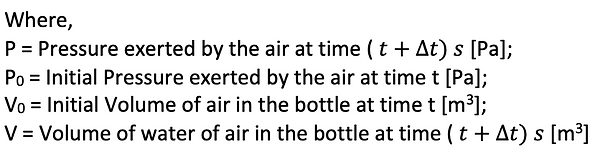
Screen Shot 2019-09-27 at 12.59.37 AM.pn

From the above equation it can be seen that both the Volume and Pressure are time dependent.

In this calculation, we assume a starting pressure of 400000 Pa for the rocket and the total Volume of the bottle is approximately 2 liters.

We also know that:

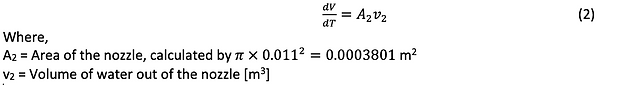
Screen Shot 2019-09-27 at 1.11.41 AM.png

From the Bernoulli’s equation, we know that:

Screen Shot 2019-09-27 at 1.14.12 AM.png

Substituting (1) in (3), we get:

Screen Shot 2019-09-27 at 1.17.02 AM.png

Since the Volume of the air in the bottle also varies as a function of time, we can write the following equation to calculate the Volume of the air (using Euler’s method):

Screen Shot 2019-09-27 at 1.22.01 AM.png

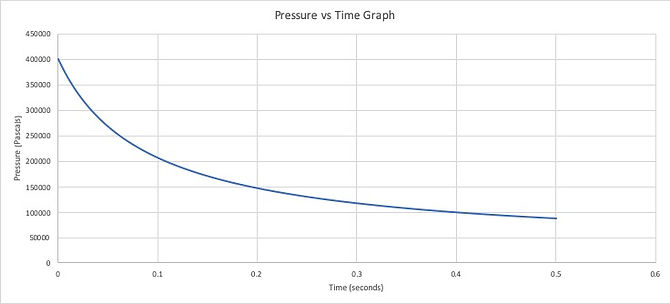
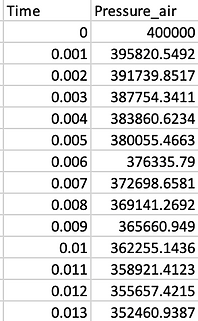
Screen Shot 2019-09-27 at 5.06.54 PM.png

In the graph above it can be seen that the pressure decreases throughout the recorded time period. This is predominantly because the air is not confined in a smaller a space and is expanding adiabatically as the water is getting expelled i.e, air is occupying a larger volume as the water is being expelled.