Temperature
Assumption:
In this calculation we are going to assume air is an ideal gas. Hence the ideal gas equation is as follows:
Where:
p = pressure
V = Volume
R = Universal gas constant
T = Temperature in Kelvin
Calculation:
As the rocket expels the water, an adiabatic expansion of air takes place. From the first law of thermodynamics it is evident that during an adiabatic expansion, Q = 0. Adiabatic processes can be represented on a Pressure-Volume diagram as shown below:
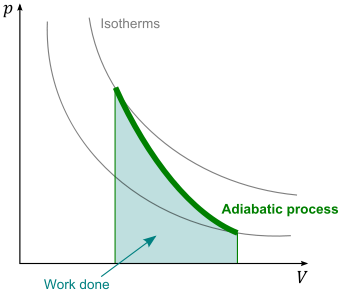
The internal energy can thus be calculated by the equation below:

Since it is an adiabatic expansion, dQ = 0
Therefore we get:
It is also known that:


Substituting the above equations in dU = -dW, we get:
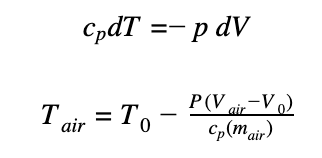
This relation can be graphically represented, as is shown below:


The starting temperature in the graph has been determined to be 298K (25°C). It can be seen that the temperature drops as the Volume increases and the water is expelled out of the rocket. This is predominantly due to the adiabatic expansion of the air. As the air has more space to fill out while the water gets expelled, there is a greater Volume. Here we have modeled the temperature as a function of time, for a period of 0.5 seconds.