Velocity
When analyzing a water-air propelled bottle rocket, many different aspects have to be taken into account. The bottle itself is a 2-liter plastic bottle with fins and a nose cone attached to help with aerodynamics. There is a specialized nozzle attached to the opening of the bottle, which is now at the bottom of the system. This nozzle is what the pressurized water and air are expelled out of causing the rocket to fly into the air.
Air is pumped into the bottle, containing water and air. As more and more air is pumped into the bottle, the pressure of the water and air starts to increase. Once the bottle is pumped to a sufficient pressure, the pressure is released and the rocket flies into the air. The pressurized air expels the mass of the water out at a rapid speed, causing thrust. This rapid movement of mass is what propels the bottle into the air.
Mass
The first step in this theoretical analysis is to determine the mass of the rocket and its contents at any given time. The bottle, fins, and nose cone all have constant mass while the water inside has a changing mass with respect to time. The equation below is the mass of the rocket and contents with respect to geometric volume and area. The z - axis is the axis running axially through the bottle. The Greek letter ρw is the density of water and A is the cross sectional area of the bottle.

Since the mass of the bottle also varies with the pressure at which mass is expelled from the bottle, the following equation is mass as a function of pressure defined by a piecewise function.
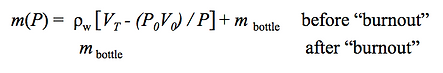
The variable VT represents the total volume of the rocket. The variables P0 and V0 represent the initial pressure and the initial volume of water in the rocket. The term “burnout” refers to the point in time when all of the water has been expelled out of the rocket.
Volume
With the bottle being filled partly with water and partly with air, initial volumes must be identified. The control volume for the amount of water in the bottle will be one third of the entire bottle’s volume, or .000666 cubic meters. This would leave the control volume for the amount of air to be .001333 cubic meters.


Shaded blue: control volume of water
= .000666 cubic meters
White: control volume of air
= .001333 cubic meters
Velocity
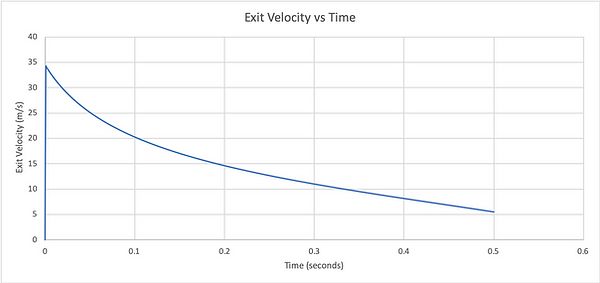
To acquire an equation for exit velocity, Bernoulli's fluid energy equation must be taken into account. Bernoulli's equation has many different aspects. Initial pressure energy, kinetic energy per unit volume, and potential energy of the fluid. When manipulating Bernoulli's equation and substituting in know constants, the following equation can be derived:

This equation shows that ve, or exit velocity of the water being expelled out of the nozzle, is a function of the differences in pressure and the density of water. It can be seen that, since P is at a maximum at time t=0, the exit velocity starts at a maximum around 35 meters per second and decreases as time goes on. This can be seen in the graph below.

Now that equations for thrust and exit velocity of the water are derived, an equation for the velocity of the rocket can be derived. Assuming that mass and volume of the water do not change instantaneously after takeoff, conservation of momentum can be applied. Since the volume of the water, the velocity it exits at, and the mass of the rocket are all known, this can be done.
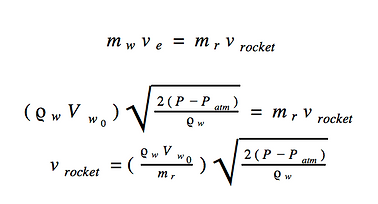
When graphing this equation, it can be seen that the velocity of the rocket starts at zero at t=0 and increases almost linearly as time goes on. The first stage of this rocket system is the water getting expelled out of the rocket's nozzle and the rocket being propelled into the air. This stage happens very quickly. And after this, the remainder of the compressed air is expelled. And finally, once all mass and air are expelled and the pressure inside the rocket is equal to the atmospheres pressure, the rocket coasts due to momentum until gravity takes over and brings it back to the ground.

